This page is under construction... Last modified July 31, 1997

Manual

Michael A. Charleston, Division of Environmental and Evolutionary Biology, Institute of Biomedical and Life Sciences, University of Glasgow, Glasgow G12 8QQ, Scotland, United Kingdom.

Tel: (0141) 330 5346, fax: (0141) 330 5971.

e-mail: m.a.charleston@bio.gla.ac.uk

Introduction to Spectrum

This section is divided into three parts: "What is a spectrum?", "What is the Closest Tree?", and "What is the Manhattan Tree?".

What is a spectrum?

A spectrum is a representation of all the inferred or estimated branch lengths of a phylogenetic tree, without the necessity of actually inferring a tree. For "good" data, that is, data which corresponds exactly to a particular phylogenetic tree without any conflict, the spectrum will show positive values only when they correspond to branches of that tree, and all the others will be zero. With n taxa and a fully resolved unrooted tree, this amounts to (2n-3) branches, n of which are pendant (often called 'leaves') and the other (n-3) of which are internal.

With n taxa there are 2^(n-1) ways of splitting the taxa into two parts, which are frequently called splits. These are all potential branches of phylogenetic trees, from which we must select a set (or sets) of splits to construct estimates of the real phylogenetic tree underlying the taxa.

You are urged to read the 'Technical bits', next.

Technical bits:

For a given set of sequences of aligned characters, each character being in one of two possible states, the sites along the sequences corresponding to hypothesized homologous characters across the taxa each divide the taxa into two sets.

Example:
As an example we consider the bacteriophage T7 data generated by Hillis et al. (1992). The binary characters in this data set are variable restriction enzyme cleavage sites. Not all data from that set are used here --- the four sites in which the relevant site was deleted in one or more of the lineages were left out. The true tree for the nine lineages is shown in Figure 1 (R is the outgroup).

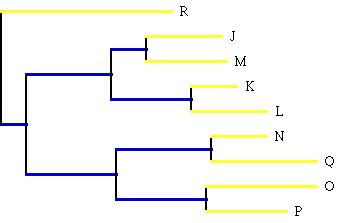
Figure 1: The branch lengths are drawn to scale with the number of changes of character state which took place during the evolution of the bacteriophage.


The raw spectrum corresponding to the T7 data is presented (apart from the zero values) in Figure 2.

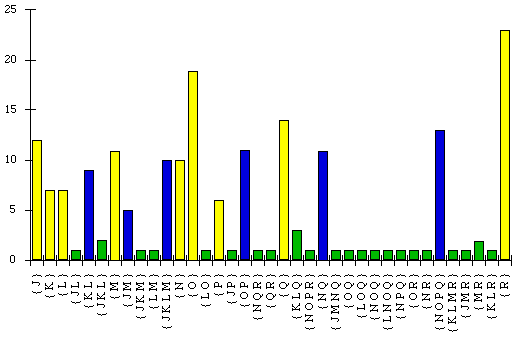
Figure 2: Raw spectrum calculated from the bacteriophage T7 data

Only those splits with at least one site supporting each are shown.


It is not always the case (in fact it is almost never the case!) that all sites in real biological data do in fact correspond to the same tree, since there may well be other random or unknown effects of the evolutionary process evinced in the data. This behaviour gives rise to the large number of splits in the above spectrum, only 6 of which can correspond to any single tree, yet which are observed in the data.

The splits are indexed using a scheme invented by M. D. Hendy (1991). First the characters are recoded if necessary so that at each site, the n-th character has state '0', and the characters which are not the same as that of the n-th are coded '1'.

The split to which the site corresponds is labelled with the binary number whose expansion is the array of characters states from the n-th down to the first, as follows: 

	Enzyme/Site HpaI/7752:
		individuals	J K L M N O P Q R
		state		+ + + + - - - - +
	Recoded to '0's and '1's: 
		011110000 (binary) = 240 (base 10).

The splits shown in Figure 2 are from the "raw spectrum" obtained from the T7 bacteriopage data. By operating on the spectrum with the Hadamard Transform of Hendy et al. (1994) we can calculate estimates of the lengths of branches within the tree which gave rise to the observed data. In this case the hypothesized model of character evolution is the very simple two-state symmetrical Markov model of Cavender (1978), in which the characters evolve stochastically in time at a constant rate, and the probability of each character changing from state '+' to state '-' is the same as the probability of changing from '-' to '+'. With such a model we can estimate the number of character state changes that must have occured on each branch of the tree to account for the observed data, 'correcting' in a sense for multiple changes.

In the ideal case with no sampling error and when the hypothesized model accurately reflects the true mechanism, then this calculation will reveal the number of character state changes per site on each branch of the tree, so the resulting spectrum will have entries which are positive only when they correspond to splits in the generating tree.

Figure 3 shows the set of entries greater than 0.0001 in the Hadamard conjugated T7 bacteriophage spectrum. To obtain positive entries for the natural log part of the transform, it was necessary to include some constant sites. In the current implementation of Spectrum, this must be by inserting columns into the original data matrix: there is as yet no mechanism for adding a number of sites which are constant otherwise.

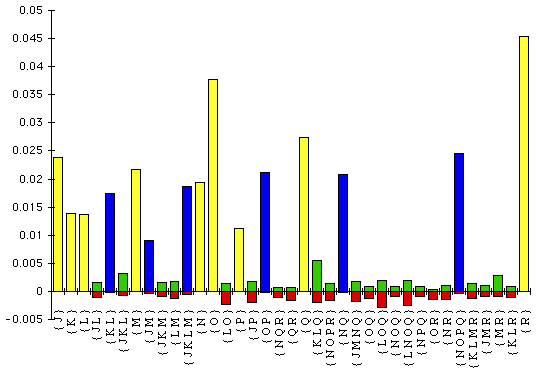
Figure 3: Hadamard log spectrum calculated from the bacteriophage T7 data

Only those splits with estimated length more than 0.0001 are shown. (The length is the expected number of character-state changes per site.) The parts in red are the relative amounts of conflict that each split shown has with the rest of the data: the singleton splits (in yellow) have no conflict, and it is clear that those splits in the true tree have very little conflict.

What is the Closest Tree?

The Closest Tree (Hendy, 1991) is that tree whose expected spectrum is the closest to that which we obtained from the data. Since the spectrum is a vector of 2^(n-1) real components, finding the closest tree is equivalent to finding the (2n-3)-dimensional hyperplane in the 2^(n-1)-dimensional real space whose axes correspond to the possible splits of the n taxa, which is the closest Euclidean distance to that point given by the spectrum. Luckily this can be achieved relatively easily with a Branch-and-Bound search, which is feasible for up to about n = 20 taxa. In this implementation of Spectrum, the maximum for n is 18, to keep memory requirements down.

What is the Manhattan Tree?

The Manhattan Tree is that tree whose expected spectrum is the closest Manhattan distance to the spectrum we obtain from the data. Another name for Manhattan distance is city-block distance. The closest tree and the Manhattan tree tend to be very similar, though finding the Manhattan tree is slightly less time-consuming.

Operation of Spectrum

The interface of Spectrum has been markedly improved in its interface, through the extensive programming help of Rod Page. The command format is now completely different, though the underlying operation remains basically the same.

Input of data

The data used by Spectrum are read in directly from an input file, which can be anywhere... The input file must be in the fast-becoming-standard Nexus format of Maddison and Maddison (1995), as is used by programs such as MacClade and PAUP.

Limitations

There are limitations with everything. Spectrum is limited in the number of taxa with which it can cope, by memory requirements. I've perhaps arbitrarily decided to keep the memory down to about 4Mb, which is of course completely miniscule when compared with, say, Microsoft Excel. If you feel that more taxa are required, let me know and I can modify the program.

Bugs

Though major improvements have been since the original versions, there may remain bugs in the code. Please let me know if and when you find any, and make sure you give details of when the problem occurs. There is a short history of updates and bug fixes which have been made to Spectrum, for interested parties.

Registration

Please register your copy of Spectrum! It costs nothing, and if you register I can keep you up to date with bugs, bug fixes, updates etc. E-mail me to register.

References

Back to my home page...